EJERCICIOS ÓPTICA

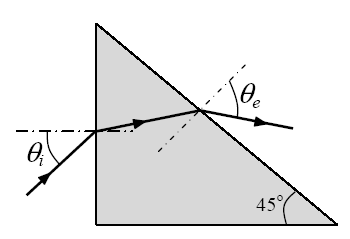
1.- Un rayo incide en un prisma triangular (n = 1,5) por el cateto de la izquierda con un ángulo q_i =30º. a) Calcule el ángulo con el que emerge por el lado de la hipotenusa. b) ¿Cuál es el ángulo de incidencia máximo para que el rayo sufra una reflexión total en la hipotenusa?
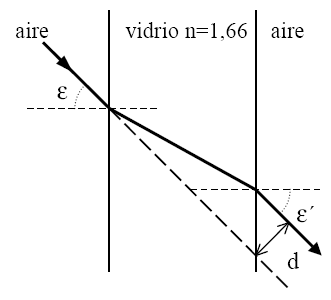
2.- Sobre una lámina de vidrio de índice de refracción n = 1,66 de caras plano-paralelas y espesor e = 5 mm, incide un rayo de luz monocromática con un ángulo de incidencia e = 45º. a) Deduzca el valor del ángulo e´ que forma el rayo emergente con la normal a la lámina. b) Calcule el valor de la distancia d entre las direcciones de la recta soporte del rayo incidente y el rayo emergente, indicada en la figura.
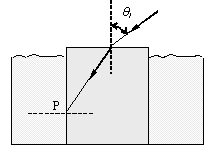
3.- Sobre una de las caras de un bloque rectangular de vidrio de índice de refracción n₂ = 1,5 incide un rayo de luz formando un ángulo q₁ con la normal al vidrio. Inicialmente, el bloque se encuentra casi totalmente inmerso en agua, cuyo índice de refracción es 1,33. a) Halle el valor del ángulo q₁ para que en un punto P de la cara normal a la de incidencia se produzca la reflexión total . b) Si se elimina el agua que rodea al vidrio, halle el nuevo valor del ángulo q₁ en estas condiciones y explique el resultado obtenido.
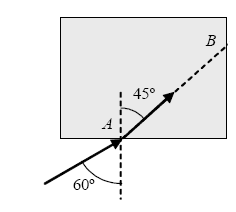
4- Sobre un prisma cúbico de índice de refracción n situado en el aire incide un rayo luminoso con un ángulo de 60º. El ángulo que forma el rayo emergente con la normal es de 45º. Determine: a) El índice de refracción n del prisma. b) El ángulo que forman entre sí la dirección del rayo incidente en A con la dirección del rayo emergente en B.
5.- Se tiene un lente convergente de vidrio de 0,6 m de distancia focal. Hallar: a) ¿A qué distancia hay que colocar un pequeño objeto en el eje para tener una imagen cuatro veces mayor que el objeto, pero invertida?. b) En el caso de que la lente sea divergente, determina la distancia a la que hay que colocar el objeto para que su imagen tenga la mitad de tamaño.